Attribute Grammars/Exercise 8: Arithmetic: Difference between revisions
From Wiki**3
< Attribute Grammars
| Line 51: | Line 51: | ||
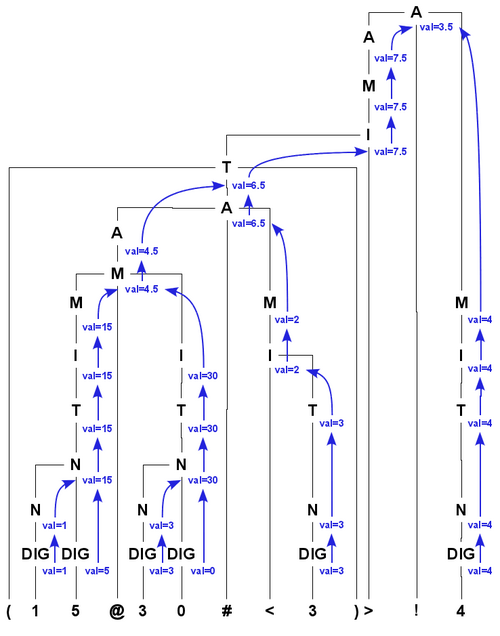
The following is the annotated tree for '''(15@30#<3)>!4'''. The green boxes represent print operations (of the displayed value). | The following is the annotated tree for '''(15@30#<3)>!4'''. The green boxes represent print operations (of the displayed value). | ||
[[Image:arithmetic-t21011-153034.png]] | [[Image:arithmetic-t21011-153034.png|500px]] | ||
=== YACC implementation === | === YACC implementation === | ||
Revision as of 18:17, 15 June 2011
Problem (in Portuguese)
(appeared in Teste 2 2010/2011)
Pretende-se criar uma gramática atributiva que calcule no símbolo inicial o valor das expressões fornecidas. As expressões são codificadas (i) como números inteiros (i.e., sequências de algarismos em base 10, cada um representado pelo token DIG, ao qual está associado o atributo val com o valor do algarismo); (ii) como somas ou subtracções unárias de uma unidade a uma expressão (respectivamente, > e <); (iii) somas ou subtracções binárias (respectivamente, # e !) de expressões; ou (iii) como percentagens de expressões (indicada como uma expressão, após o operador @).
Os operadores unários têm precedência sobre todos os operadores binários. O operador @ tem precedência superior aos operadores # e !. Todos os operadores binários são associativos à esquerda. Podem ser utilizados parênteses para alteração das precedências.
Examples
- 37 é representado pela sequência DIG DIG (o primeiro token tem o atributo val com valor 3 e o segundo com o valor 7).
- 4> tem o valor 5
- <3 tem o valor 2
- 36@20 tem o valor 7.2
- (24>#25)@20#7!<15#6 tem o valor 9
Questions
- Identifique a gramática atributiva correspondente ao problema. Descreva o significado e o tipo de cada atributo. Que tipo de gramática obteve?
- Identifique a árvore de sintaxe decorada e o grafo de dependências para a frase (15@30#<3)>!4 (valor 3.5).
- Escreva uma especificação YACC que implemente a gramática descrita em 1. Codifique toda a especificação (incluindo as zonas de declarações e de regras) e todas as funções auxiliares. Não utilizar variáveis globais.
Solution
The problem has a simple solution, if you remember to define a non-terminal symbol for each precedence.
<text> P -> A { std::cout << "RESULT: " << (P.val = A.val) << std::endl;}
A_0 -> A_1 # M { A_0.val = A_1.val + M.val; } A_0 -> A_1 ! M { A_0.val = A_1.val - M.val; } A -> M { A_0.val = M.val; }
M_0 -> M_1 @ I { M_0.val = M_1.val * I.val / 100; } M -> I { M_0.val = I.val; }
I -> T > { I.val = T.val + 1; } I -> < T { I.val = T.val - 1; } I -> T { I.val = T.val; }
T -> N { T.val = N.val; } T -> ( A ) { T.val = A.val; }
N -> DIG { N.val = DIG.val; } N_0 -> N_1 DIG { N_0.val = N_1.val * 10 + DIG.val; } </text>
All attributes are synthesized (S-attributed grammar): val encodes the value associated with each grammar symbol.
Semantic Tree
The following is the annotated tree for (15@30#<3)>!4. The green boxes represent print operations (of the displayed value).
YACC implementation
A YACC specification can be obtained by adapting the grammar above: <text> %{
- include <cstdlib>
- include <iostream>
inline void yyerror(const char *msg) { std::cout << msg << std::endl; } %} %union { int i; double d; } %token DIG %type<d> expr num %left '#' '!' %left '@' %nonassoc '<' '>' %% print: expr { std::cout << "RESULT: " << $1 << std::endl;}
;
expr: num { $$ = $1; }
| '<' expr { $$ = $2 - 1; }
| expr '>' { $$ = $1 + 1; }
| expr '#' expr { $$ = $1 + $3; }
| expr '!' expr { $$ = $1 - $3; }
| expr '@' expr { $$ = $1 * $3 / 100; }
| '(' expr ')' { $$ = $2; }
;
num : DIG { $$ = $1; }
| num DIG { $$ = 10 * $1 + $2; }
;
%% extern int yylex(); extern int yyparse(); int main() { return yyparse(); } </text>
This specification uses the following Flex specification (others could be used -- indeed, this is a very simple definition): <text> %option debug noyywrap %{
- include "y.tab.h"
%} %% digit: yylval.i = atoi(yytext); return DIG; [@()<>!#] return *yytext; .|\n ; %% </text>