Theoretical Aspects of Lexical Analysis

Lexical analysis, the first step in the compilation process, splits the input data into segments and classifies them. Each segment of the input (a lexeme) will be assigned a label (the token).

In this case, we will be using regular expressions for recognizing portions of the input text.

Regular Expressions

Regular expressions are defined considering a finite alphabet Σ = { a, b, ..., c } and the empty string ε:

The languages (sets of strings) for each of these entities are:

• {ε}, for ε
• {a}, for an entry a in Σ

The following primitive constructors are defined:

• concatenation
• alternative
• Kleene-star (*)

Extensions (derived from the above):

• Transitive closure (+) - a+ ("one or more 'a'")
• Optionality (?) - a? ("zero or one 'a'")
• Character classes - [a-z] ("all chars in the 'a-z' range" - only one character is matched)

Recognizing/Matching Regular Expressions: Thompson's Algorithm

Since we are going to use sets of regular expressions for recognizing input strings, we need a way of implementing that functionality. The recognition process can be efficiently carried out by finite state automata that either accept of reject a given string.

Ken Thompson, the creator of the B language (one of the predecessors of C) and one of the creators of the UNIX operating system, devised the algorithm that carries his name and describes how to build an acceptor for a given regular expression.

Created for Thompson's implementation of the grep UNIX command, the algorithm creates an NFA from a regular expression specification that can then be converted into a DFA. It is this DFA that after minimization yields an automaton that is an acceptor for the original expression.

The following sections cover the algorithm's construction primitives and how to recognize a simple expression. Lexical analysis such as performed by flex requires several expressions to be watched for, each one corresponding to a token. Such automatons feature multiple final states, one or more for each recognized expression.

Building the NFA: Thompson's Algorithm

Thompson's algorithm is based on a few primitives, as show in the following table:

Example	Diagram	Meaning
<amsmath>\epsilon</amsmath>		Empty expression (in the following diagrams, empty expressions will be represented by unlabeled edges).
<amsmath>a</amsmath>		One occurrence of an expression.
<amsmath>a*</amsmath>		Zero or more occurrences of an expression: this case may be generalized for more complex expression. In this case, the complex expression will simply take the place of <amsmath>a</amsmath> arc in the diagram.
<amsmath>ab</amsmath>		Concatenation of two or more expressions: the first expression's final state coincides with the second's. This case, like the previous one, may be generalized to describe more complex concatenations.
b</amsmath>		Alternative expressions: the to initial states and the final states of each expression are connected to two new states. Both expressions may be replaced by more general cases.

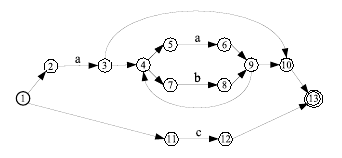
Complex expressions are built from these primitives. The following diagram corresponds to the expression a(a|b)∗|c (note how the Kleene-star operator affects an alternative group):

Building DFAs from NFAs

NFAs are not well suited for computers to work with, since each state may have multiple acceptable conditions for transitioning to another state (searching and backtracking would be needed to directly using an NFA). Thus, it is necessary to transform the automaton so that each state has a single transition for each possible condition. This process is called determination. The algorithm for transforming an NFA into a DFA is a simple one and relies on two primitive functions, move and ε−closure.

The move function is defined over a set of NFA states and input symbol pairs and a set of NFA states sets: for each state and input symbol, it computes the set of reacheable states. As an example consider, for the NFA in the previous automaton:

• move({2}, a) = {3}
• move({5}, a) = {6}
• move({11}, a) = {}

The ε−closure function is defined for sets of states: the function computes a new set of states reachable from the initial set by using only all the possible transitions to other states (including the each state itself), as well as the states reacheable through transitions from those states. Thus, considering the previous NFA, we could write:

• ε−closure({1}) = {1, 2, 11}
• ε−closure(move({2}, a)) = ε−closure({3}) = {3, 4, 5, 7, 10, 13}

With the two above functions we can describe a determinization algorithm. The input for the determinization algorithm is a set of NFA states and their corresponding transitions; a distinguished start state and a set of final states. The output is a set of DFA states (as well as the configuration of NFA states corresponding to each DFA state); a distinguished start state and a set of final states.

The algorithm considers an agenda containing pairs of DFA states and input symbols. Each pair corresponds to a possible transition in the DFA (possible in the sense that it may not exist). Each new state, obtained from considering successful transitions from agenda pairs, must be considered as well with each input symbol. The algorithm ends when no more pairs exist in the agenda and no more can be added.

DFA states containing in their configurations final NFA states are also final.

Step 1: Compute the ε−closure of the NFA’s start state. The resulting set will be the DFA’s start state, I₀. Add all pairs (I₀, α) (∀_{α∈Σ}, with Σ the input alphabeth) to the agenda.

Step 2: For each unprocessed pair in the agenda (I_n, α), remove it from the agenda and compute ε−closure(move(In , α)): if the resulting configuration, I_n+1, is not a known one (i.e., it is different from all I_k, ∀_k<n+1), add the corresponding pairs to the agenda.

Step 3: Repeat step 2 until the agenda is empty.